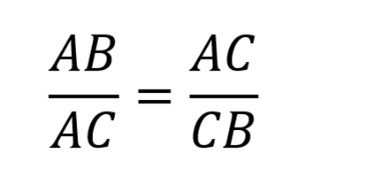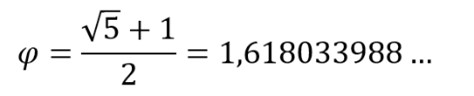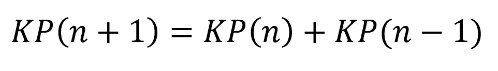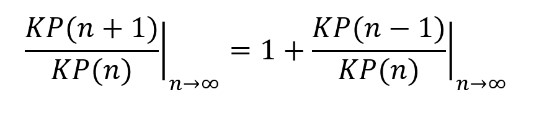HERR NILSEN, OSLO, LØRDAG 1. FEBRUAR 2025: Guddommelig musikk og perfekte snitt, og da snakker vi ikke om volumet på et øl-glass. En snitt øl skal være 25 cl, en halv halvliter, omtrent tilsvarende en half pint, som er litt over 28 cl. Og ja, det er hankjønn. Det heter absolutt ikke ‘et snitt øl’. Snittet er det som deler de to delene, en snitt er en av de fraskilte delene. Så enkelt er det. Et snitt deler en snitt fra en annen snitt.
Er du kun interessert i å lese om konserten? Gå da direkte til konsertomtalen.
Skal det være en snitt?
Men perfekte snitt har altså ingen ting med øl å gjøre – annet enn i overført betydning. Hva er dette perfekte snittet, spør du? Du lærte det vel en gang på skolen: Start med et vilkårlig linjestykke. Kall endepunktene A og B. Plasser et punkt på linjestykket mellom de to endepunktene, og kall det C. Vi velger å plassere snittet C slik at den lengste snitten av linjestykket er AC. Punktet C er altså nærmere B enn A.
Det perfekte snittet av det hele linjestykkket AB er da et snitt C, plassert slik at lengdene av AB og snitten AC og snitten CB har følgende egenskap:
Forholdet mellom lengden av hele linjestykket AB, og den lengste snitten AC, er lik til forholdet mellom den lengste AC, og den korteste snitten CB.
Om du nå lager et rektangel av de to snittene, med AC som lengden på to motstående sider og de to andre sidene lange som enten CB eller AB, får du i begge tilfeller det som allerede i renessansen ble ansett som det estetisk mest tilfredsstillende forholdet mellom sidene i et rektangel. Slike rektangler ble da også tidlig brukt av kunstnere og arkitekter i deres konstruksjoner.
Det er ikke komplisert å regne ut verdien av dette forholdet. Kan du løse en kvadratlikning, i dette tilfellet likningen x2 – x – 1 = 0, kan du finne forholdstallet. Denne kvadratlikningen sier akkurat det samme som forholdet mellom linjestykkenes lengde over.
Det er konvensjonelt å betegne løsningen på dette, det perfekte snitt, med den greske bokstaven fi, φ. Forholdet mellom det lange og det korte linjestykket, altså løsningen på den kvadratiske likningen i forrige avsnitt, er x = φ, der φ er denne verdien,
Dette tallet er det gyldne forholdet, det perfekte snitt. Siden kvadratroten av 5 er et irrasjonalt tall, er også forholdstallet i det perfekte snittet, selv et irrasjonalt tall – slik som også π = 3,141592…. er.
Men tallet har i tillegg en fascinerende egenskap som følger av direkte av den kvadratiske likningen over. Avstanden mellom det gyldne snitt og den inverse av tallet er 1, altså
Det gyldne er det guddommelige
To italienske matematikere kan på svært forkjellige måter knyttes til dette snittet. I 1509 kalte Luca Pacioli dette forholdet for ‘det guddommelige snittet’. Og det samtidige flågvitet Leonardo da Vinci brukte det aktivt i sin kunst. Sjekk maleriene Il Cenacolo (Nattverden) og ikke minst, La Gioconda (Mona Lisa). Navnet ‘det gyldne snittet’ fikk dette forholdstallet først på 1800-tallet.
Men også en annen Leonardo er relevant. For tre hundre år før Leonardo da Vinci og Luca Pacioli, formulerte matematikeren som fikk tilnavnet Fibonacci et tankeeksperiment. Navnet han seinere er kjent med, er laget fra filius Bonacci, som visstnok kan leses som ‘sønn av fin familie’. Men dette var også en Leonardo – Leonardo Pisano het han. Han ble i voksen alder matematiker, og importerte mye viten fra arabisk og hinduistisk matematikk til Europa. Now av det han lærte gjorde at han kunne beskrive et tankeeksperiment.
Dette er som følger. Anta at kaniner har en livssyklus som kan beskrives som å skje i hele perioder. Anta også at kaniner lever uendelig lenge. (Bare så det er sagt, dette er et tankeeksperiment, så vi kan gi kaninene vilke egenskaper vi bare vil.) Sett av en innelukket eiendom. Plasser to nyfødte kaniner på denne eiendommen.
Etter én periode, la oss kalle det en måned, er de kjønnsmodne og parrer seg. I slutten av neste måned får de to nye avkom. Det første paret parrer seg umiddelbart igjen. Etter en ny måned er også det nye paret kjønnsmodne og parrer seg, mens det opprinnelige paret setter til verden to nye avkom og parrer seg igjen. Og slik fortsetter det.
Spørsmålet er da, hvor mange par kaniner er det etter n perioder, eller måneder? Svaret er at antallet par er gitt ved tallene i Fibonacci-rekka, en tallrekke som Leonardo Pisano hadde lært fra sitt møte med hindu-arabisk matematikk. Ved slutten av både første og andre periode er det ett par. Ved slutten av tredje periode er det to par. En periode seinere er det tre par. Deretter fem par. Så blir det åtte par, for så å bli til 13 par. Med andre ord,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Dette er Fibonacci-rekka: Det er en rekke som du kan finne igjen en lang rekke steder i naturen, og også i kunsten. Som i Hokusais fantastiske studie, Den store bølgen ved Kanagawa. Eller i blomsterbunnen av en solsikke.
Kaniner overalt
La oss kalle antallet kaninpar etter n måneder for KP(n). Med andre ord er KP(1) = KP(2) = 1, KP(3) = 2, KP(4) = 3, osv. Vi ser også, av tallrekka over, at KP(10) = 55.
Det ser så uskyldig ut, men kraften i denne tallrekka er stor. Ved utløpet av den tiende måneden er det altså 55 kaninpar. Videre, ved slutten av det første året er det 144 kaninpar. Etter to år er det 46 369 kaninpar. Etter bare fire år passerer det 4,8 milliarder kaninpar.
Et par måneder seinere er det flere kaninpar enn det er mennesker på jorda. Ti år etter at kaninene ble satt ut, vil det være 5,36 kvadrilliarder kaninpar – et tall med 25 siffer! Et tall som til sammenlikning er ti millioner ganger større enn antallet sekunder som er gått siden Big Bang! Det er et tall som er større enn antall stjerner i hele det observerbare universet rundt oss. Vi kan jo lett tenke oss hvor fortvilede bøndene i Australia var, som satte ut de første kaninene! De første kaninene slapp ut i villmarka etter 1788. Ti år seinere var ikke det 19. århundret begynt en gang!
Av tallene ser vi at vi kan beskrive rekka av Fibonacci-tallene, KP(n), slik:
Hvert tall i serien er summen av de to foregående. Det er ikke komplisert å bevise denne sammenhengen heller.
Nå kommer det som vi virkelig kan kalle matematisk skjønnhet. Beregn nå tallforholdet mellom to etterfølgende tall i rekka, og beregn dette forholdet når antallet måneder som er gått, n, blir stort.
Vi ønsker altså å finne et forholdstall som oppfyller denne likningen
Men når n er svært stor, vil det siste leddet på høyre side etter hvert være det samme – svært nær – det inverse av uttrykket på venstre side av likhetstegnet. Med det blir denne likningen altså etter hvert den samme likningen som vi i stad fant at det perfekte snittet φ oppfylte!
Konklusjonen er åpenbar: Forholdstallet mellom to tall i Fibonacci-rekka nærmer seg altså det gyldne snitt etter som antallet perioder blir stort! Og med det: En tallserie – altså aritmetikk – er knyttet sammen med geometrisk form – og videre med estetikk! Dette er skjønnhetens vesen i et nøtteskall. Skjønnhet er det som knytter to eller flere svært forskjellige livsverdener sammen på spennende, ukjente måter. Skjønnhet er det som framstår som enkelt, men som ved fordyping viser seg å ha et rikt og variert innhold. Skjønnhet har fruktbarhet og konnektivitet, fecunditatum & conexionem. In simplicitate forma – i det enkle er det skjønne, det velformede.
De perfekte forhold i trioen
Det er derfor overhodet ikke overraskende at den danske pianisten og maleren Carsten Dahl kaller sin trio for Carsten Dahl Golden Ratio Trio. Sist høst slapp Dahl et album, Interpretations – The Norwegian Sessions på Storyville, som tittelen antyder spilt inn i Norge. Albumet er innspilt i Asker og Oslo, en del på Musikkloftet til Vidar Lunden i Asker, vest for Oslo, andre del i Thor Bjørn Nebys studio på Ris, vest i Oslo. Vår anmeldelse av albumet kan du lese her.
Med seg har han bassisten Daniel Franck, og trommeslager Martin Andersen. Begge sentrale aktører i den danske jazzen. Første settet blir en kraftfull reise i trioens frislippte improvisasjoner over smellvakre tema skrevet av de tre sammen, eller hver for seg. Carsten Dahl spiller på Herr Nilsens Steinway stå-opp-piano, et piano som krever en fast hånd og kraftfulle anslag. Det blir en pianolyd ut i lokalet som muligens er i hardeste laget, der de finere nyansene i Dahls spill blir borte. Nyanser som et instrument med ‘raskere’ og ‘finere’ mekanikk måtte til for å fange opp. Men Dahl lar seg ikke hemme av dette.
Første strekket som jeg oppfatter som en kollektiv improvisasjon omfatter også et lite hint av «Someday My Prince Will Come», før vi vandrer inn i …. drømmeland, drammølend, dremmalønd, dramlenald, dladmemøra, remaldmørd … Daniel Francks linjer er som solgult fløtesmør på en ristet skive grovbrød en sommeraften, mens vindens rislen i strågul marehalm akkompagnerer landskapet og oss. Andersens spill er linjeførende og stryker deg både medhårs og mothårs, fra full tenning på alle 12 til vispende, viskende, piskende snert.
Der svinger også en liten dans med Monk innom, du veit, når Thelonious Monk reiser seg fra flygelet under en av de øvrige musikernes soli, og dansevandresvinger seg rundt flygelet. Aldri påtrengende, bare full av livsglede og innlevelse i musikken. Det er så deilig, at.
Fra Köln til Oslo
Når Dahl legger i vei med pianosolo, er det til tider lett å assosiere til pianosolo-framføringene til Keith Jarrett på 1970-tallet. Det er jo heller ikke mange dagene siden innspillingen av den mest-selgende plata i ECM-katalogen, The Köln Concert, ble femti år. 24. januar 1975 satte Jarrett seg ned ved et andrerangs flygel i Oper Köln og spilte inn det som ble en dobbelt-LP.
Jeg har lenge opplevd at denne innspillingen er underordnet den solokonserten som ble sendt på radio av Radio Bremen ni dager seinere. Dahl-konsertens etterfølgende dag, søndag 2. februar 2025, er det femti år siden Jarrett spilte i storsalen i Die Glocke i Bremen. Radioopptaket er strålende, og spillet er minst like medrivende som i Köln. Han starter samme sted, i B♭, men utvikler det annerledes. Det kan jo ha sammenheng med at Köln-konserten lenge ble spilt på repeat, og at jeg etter hvert fikk nok. Det kan være grenser for hvor mange ganger det er interessant å gå langs den samme skogsstien, selv når det er gjennom en underskog med masser av biologisk liv.
Carsten Dahl har aldri lagt skjul på sin mangeårige psykiske lidelse, det er vel ett av de områdene der jeg også har funnet igjen meg selv i en musikers musikk. Komposisjonen «Savant» gjenspeiler den diagnosen han etter mange år uten avkreftende bekreftelse, fikk for sine lidelser. Her legger han inn fugastiske kontrapunkt som selvfølgelig minner oss sterkt om fugatorenes fugomenalistiske fuguoser, han som virkelig satte fluktens kunst på det musikalske kartet.
Johann Sebastian B lagde seg en signatur av to kryssende sett av notelinjer, med en nøkkel på hver av de fire endene. I midten, på den midterste notelinja er det angitt midt i krysset en heltone. Første nøkkel er en G-nøkkel, med toneart angitt som F-dur/d-moll. Tonen er altså den som vi til vanlig angir som B♭. Resten er angitt uten fortegn. Går vi med klokka, er neste nøkkel en tenornøkkel, en C-nøkkel i nest øverste etasje. Tonen er altså en A. Neste er en alt-nøkkel, en C-nøkkel i midt-etasjen, vi leser altså en C. Siste, og nederste nøkkel er igjen en G-nøkkel på sedvanlig plass, med opphevelse på midtlinja, der ♭-en var på første ende. Tonen er altså en B.
Mellom bekker og daler
Hva har vi da? B♭-A-C-B. Hva betyr det? Det ser jo helt meningsløst ut, ikke sant? Eller …? For dette kan du tolke med det du lærte på barneskolen: Dette er jo med de angloamerikanske toneangivelser aom dominerer i jazzen. I sang- og musikkundervisningen lærte du en gang at det var den tysk-kontinentale navngivingen, som er/var den tradisjonelle her i Skandinavia. B♭ noteres da som B, og B som H. Hva-har-vi-da? Jo, B-A-C-H.
Og begynner du å lete, finner du dette lille firetonige motivet igjen i en lang rekke komposisjoner av fader Bach. Ett av flere eksempler: I den andre Brandenburger-konserten, mot slutten av første sats, legger Johann Sebastian inn dette i bassen over fire takter (taktene 109-12). Påskeegg kalles dette i programvare og dataspill. En skjult henvisning til den eller de som har konstruert programmet, og som kan finnes av de som vet hvor og hvordan de skal lete.
Hans sønner, Carl Philip Emanuel og de andre, gjør det samme og fletter inn det samme påskeegget. Wiener-gutta, ikke klassikerne, altså – men Arnold Schönberg og hans kumpaner, den såkalte andre Wien-skolen, flettet dette også inn. Men det er jo klart at dette kromatiske motivet (med tre etterfølgende halvtrinn) er lettere å gjenskape i en kromatisk tolvtonekomposisjon enn en diatonisk sammenheng.
Slik kunne vi fortsette, men vi gjør det ei. Uansett, D-A-H-L kunne jo med litt anstrengelse også fungere som et lite motiv. Om vi velger H som grunntone og bygger en lokrisk skala over den, har vi tonene D-A-H og L for lokrisk. Dessuten er jo dette en skala med flat femmer (F). Flate femmere er jo svært kjennetegnende og populære i den bopbaserte musikken. Slik kan vi leike. Og det er jo i leiken livet lever. Det vet Carsten Dahl og det vet vi.
Tilgivelse i Tunisia
Om første sett ble en vandring i et frittgående landskap med frie assosiasjoner og krumspring, ble andre settet totalt annerledes. Men først, leiken og livet er ikke bare snakk om latter, leven og moro. Den danske fioinisten Kristian Jørgensen døde nylig, bare 57 år gammel. Han var jevnaldrende med Carsten Dahl og de var gode venner. Første spilte tema etter pausen var en smertelig vakker komposisjon som Dahl har dedikert til Kristian Jørgensen.
Andre låt var «Ways to Forgive», et tema som kanskje mange av oss kunne hatt nytte av å tenke over. Dahl forteller at den er skrevet «…ud fra de mange skilsmisser i mit liv …».. Og derfra vandrer vi ut i et landskap av vakre versjoner av noen av jazzens mange standardlåter.
Først ut er John Coltranes monumentale «Giant Steps», ei låt som på et vis brakte hard-bopen til sin aller ytterste konsekvens, der opplevelsen av en grunnleggende tonalitet ble nesten oppløst. Heftig spilt der av trommeslager Andersen.
Det er ikke mange konserter Dahl spiller uten at han er innom «Blame it on My Youth». Vi får en smeltende-øm versjon her i dag, før trioen dundrer ut i «Night in Tunisia», den som i følge Art Blakey, Dizzy Gillespie fant «… at the bottom of a garbage can»! Andersen viser seg å ha en livlig munnhule, og vi kan lukte smellet i stikkene med romlyd fra åpen munn helt hit vi sitter.
Alt jeg er, det er perfekt
En svevende, levende og sprelsk versjon av «All the Things You Are» avslutter den ordinære delen av settet og konserten. Som ekstranummer får vi først, ikke upassende i og med at vi i dag har begynt på måneden februar, «My Funny Valentine». I Lorentz Harts tekst lyder jo der, «… you’re my favorite piece of art», og da er vi jo akkurat tilbake der vi startet med det gyldne snitt.
Nå er vi jo i så godt humør, og varmen slår imot oss, så når de sveiver innom «Summertime», «… where the livin’ is easy», så er vi med. Selv om livet jo var alt annet enn «easy» i den fantastiske operaen Porgy and Bess av George Gershwin, med libretto av Ira Gershwin i samarbeid med han som skrev boka Porgy som dannet utgangspunktet for operaen, DuBose Heyward. En avsluttende «Over the Rainbow» slutt- og fullfører så et glitrende andresett, og en strålende konsert en lørdagsettermiddag i begynnelsen av februar i sentrum av Oslo.
To svært forskjellige sett. En konsert er jo på mange måter å anse som en storform. Første underdelingen er da i to sett. Hvert sett er selv en suite med et varierende antall satser. Som sagt, svært forskjellige, men allikevel komplementære, som danner en lang fortellende bue. To sett som forteller svært forskjellige historier, men som til sammen skaper en helhetlig reise. Jeg tror ikke det var tiltenkt fra begynnelsen, men ble en del av dynamikken som vokste fram i løpet av denne ettermiddagen.
Så kommer da om trioen med det gyldne snitt også holdt seg til det perfekte snitt i utøvelse, i framføring? Lengden av andre sett, målt i minutter, i forhold til første settets lengde, er 1,589…. Som vi husker beregnet vi det perfekte snittet φ til 1,61803… Dette er jo bemerkelsesverdig nær forholdet mellom de to settene.
Det manglet altså kun 1 minutt og 12 sekunder på andre sett for at forholdet mellom settene skulle være det gyldne forholdet! Det må vi jo si er passende for en trio som kaller seg
Carsten Dahl Golden Ratio Trio.
Tekst og foto: Johan Hauknes